1. Introduction
To SodaStream or not to SodaStream
Why don’t you use SodaStream our friend Chuck asked me, as I put a store-bought bottle of soda water on the table. Because, I said, SodaStream has factories in the occupied West Bank, an occupation I oppose, and that I do not want to support financially. Chuck, who is of Israeli origin like us, said that he agrees with my views on this, but that on the other hand SodaStream is environmentally better because you do not consume plastic bottles, and for him that’s more important. This leaves me with a dilemma, to use SodaStream or bottled seltzer, each of these decisions leaves me frustrated. Of course, I could choose to drink tap water, but I really like soda water, which is another (maybe less righteous) constraint.
The SodaStream dilemma is an example of the types of decisions that we face, where each option leaves us unsatisfied, or frustrated. In many decisions that we make we try to satisfy or even optimize our interests or values or both. In many cases though these different factors are inconsistent with each other, and decisions that maximize one might reduce the other. Given such different and possibly inconsistent constraints, each decision will violate some of the constraints. Violating such constraints is likely to leave us frustrated. I contend that in this world, many of the decisions that we make fall into the category in which external constraints do not allow us to obtain all our goals or desires. Such a world falls into a class of systems that physicists call frustrated systems1. Frustrated systems in physics, have distinct general properties, and I will argue here that this analogy with physics can contribute to how we understand the social world.
Questions regarding frustrating decisions only have a broader impact if my decisions have an impact on the final outcomes. For example, if my decision to use SodaStream or not has an impact on middle eastern politics, or on the environmental fate of the planet. In truth my decisions in the SodaStream example, and in many other cases, will have at best only a very small impact on many of these problems2. However, let’s assume for now that my decisions can affect the decisions of others, and this might lead to some cascade that could possibly result in noticeable changes to the world. This might be a stretch for this example, because the system is so large, and I am so small. However, even in large systems, if what I do somehow becomes correlated with what many others do, my choices might matter.
The central goal of this text, apart from trying to justify my decision about which soda to drink, is to claim that such frustrations are actually a central component of how the social world works, and to try and understand what this implies. In order to understand this, I intend to use simple toy-models of the world borrowed from Physics. In other words, my approach here is to gain some insight about our very complicated social world, by using what I consider the ‘simpler’ world of model systems explored by physicists.
I know that when I say the words ‘simple’ and ‘physics’ in the same breath some people might immediately switch off. I promise here to do my best to explain these systems intuitively, without using complex mathematics. In following sections I try to explain some of the rudimentary physics of frustrated systems, without using much math. There are some optional math boxes in the appendix, but they will not be essential for understanding the setup of the models presented, and their results. They will be essential if one wants to understand in detail how such models are constructed, and possibly the justification for some of the general theoretical claims made.
I make the strong claim here, that based on the two simple assumptions, outlined above, one can already draw significant conclusions about the nature of the world we live in. The first assumption is simply that many of the decisions we make in this world are inherently and unavoidably frustrating. The second assumption is that our decisions have some effect on the world, and therefore our decisions affect other people’s decisions. These two assumptions imply that the social and political world we live in is inherently a frustrated system.
Once we recognize the world as a frustrated system, we can draw several very general qualitative conclusions. First, in such a frustrated system there are many possible outcomes that can reduce people’s frustrations but not eliminate them. In frustrated systems there are ways to reduce average frustrations, but compromises are essential, as there is no way to totally eliminate all frustrations. If in such a world there are significant power differentials, frustrations will in general be much larger than in a more egalitarian world. Finally, the purest approach which tries to eliminate all frustrations, which tries to achieve utopia, is not only destined to fail, but also to make matters worse.
1.1 Are frustrations inevitable?
While maybe not all decisions have the same life-changing consequences as the decision about which soda to buy, many of the decisions we make do share a central characteristic of that decision. For many of the dilemmas we face, each possible choice leaves us somewhat frustrated. The central premise of this manuscript is that in the world we live in, many decisions are inherently frustrating. I do not prove this assumption here and don’t know if it can be proven. I agree that it’s reasonable to question such an assumption. To address such concerns, I devote this section to providing some examples that demonstrate how prevalent such frustrating decisions are.
Marco and Sam want to buy a home
Examples of frustrating decisions span from the personal to the political, from choices we make that mostly affect our own life to choices made that can affect society at large.
Marco and Sam, a married couple, live in a small rented two-bedroom apartment in the city. The location is convenient. Sam can walk to work, and Marco can take a bus. They own one car but use it primarily on the weekends to go for trips and vacations, and to do some of their shopping during the week. They have one daughter who is two years old, and they will soon have another son. They would love to buy an apartment or a house, and it’s hard for them to decide whether to buy an apartment in the city, or a house in the suburbs.
They love many aspects of city life, and although both grew up in the suburbs, Sam has lived in this city for more than 15 years and really does not want to leave. They are both employed in well-paying jobs. However, if they buy an apartment in the city, it would be as small as the one that they currently rent, and it will stretch their budget. However, they really dislike the small size and high cost of their apartment, and the fact that it has no garden. They didn’t really mind the small size in the past, but since their daughter was born, and since that they will soon also have another child, this has become a problem. This was especially difficult during the peak of the covid pandemic, when they even left the city for a while and stayed with Marco’s mom for more space. If they had their own garden, it would be so much easier, especially with a young family.
They could afford a house with a nice garden in the suburbs, that house would also be cheaper. However, living in the suburbs would require a commute of nearly an hour in each direction, for both of them. If they move, they will also need to get another car, which will also cost money and cut into the savings from buying the cheaper suburban house. They will also need to spend more money on gas, and their children would stay at daycare for more hours. Even though they would like to spend more time with their children in the garden, they will actually spend more time in their car and have very little time remaining to be in garden.
So clearly, Sam and Marco face a frustrating decision; a decision similar to one many people face. This decision though seems totally personal, and not to affect anyone apart from their family, and maybe a few friends. However, there is another dimension to their decision. If they do move to the suburbs they will drive more, and this will contribute to greenhouse gas and to global warming. They will also be using the roads more, roads that are built with tax dollars. If they move to the suburbs, two more cars will be added to the daily commute, and this will increase commute times for other people who live in the suburbs. On the other hand, if they stay in this expensive city, with its limited supply of houses, they will contribute to an increase in the house prices in the city. This increase will affect for other people as well. It will make it harder for people who lived in the city for many years, and for families who have lived there for many generations to still afford living in the city.
Now seriously, Sam and Marco are one couple, how much impact do they really have on global warming, how much impact do they have on the prices of apartments? Their impact at best is marginal, just like the impact of our own votes on election results is marginal. However, if their decisions are correlated with the decisions of many others in the population, the collective effect of their decision would be quite significant. Decisions are often correlated, for many reasons, but to a large extent because the forces affecting the decisions of many different people are quite similar.
I have shown here an example of a frustrating personal decision that is similar to one many of us have to make. Such personal decisions, if they are correlated with decisions many people make, can have a significant impact on the world. These decisions also in turn can affect the decisions of many other people. For example, if Marco and Sam move to the suburbs, and many other people do as well, this will increase the commute times, and this in turn can have an impact of the decision that another couple, Jessy and Jane, will make in a few years’ time on whether to return to the city. Their decision might also cause new road construction, affecting global warming, and also increasing everyone’s tax rates, including the tax rates of those who stayed in the city.
Better than a dog anyhow
“In 1838 Charles Darwin considered whether he should get married or not, he compiled two handwritten lists of pros and cons. An image of the note is in figure 1.1, they are quite hard to read. These are the contents of this pro/con list:
“Marry
Children -- (if it Please God) -- Constant companion, (& friend in old age) who will feel interested in one, -- object to be beloved & played with. -- -better than a dog anyhow. -- Home, & someone to take care of house -- Charms of music & female chit-chat. -- These things good for one's health. -- but terrible loss of time. -
My God, it is intolerable to think of spending one’s whole life, like a neuter bee, working, working, & nothing after all. -- No, no won't do. -- Imagine living all one's day solitarily in smoky dirty London House. -- Only picture to yourself a nice soft wife on a sofa with good fire, & books & music perhaps -- Compare this vision with the dingy reality of Grt. Marlbro' St.
Not Marry
Freedom to go where one liked -- choice of Society & little of it. -- Conversation of clever men at clubs -- Not forced to visit relatives, & to bend in every trifle. -- to have the expense & anxiety of children -- perhaps quarelling -- Loss of time. -- cannot read in the Evenings -- fatness & idleness -- Anxiety & responsibility -- less money for books &c -- if many children forced to gain one's bread. -- (But then it is very bad for ones health to work too much)
Perhaps my wife wont like London; then the sentence is banishment & degradation into indolent, idle fool – “
From the list we can see clearly that this was a frustrating decision. Most of us probably do not make such lists, most of our decisions on such issues are probably more intuitive and emotional and to me it seems that it is quite unlikely that Darwin really used this list. Darwin seems to have had better arguments for not marrying, given that one argument for marrying was “better than a dog anyhow”. Yet, he got married a short time later.
This decision, whether to marry or not, is a decision many people make, maybe often not explicitly, but rather implicitly in their actions, and many people nowadays do not get married. As a society the individual decisions to marry or not, if they are correlated with other people’s decisions, can have a collective impact. Indeed, many less people today get married than a couple of decades ago, and many unmarried people have children. The impact of the drop of marriage rates on the wellbeing of people and children in our society is a highly debated topic and is not the focus of this project. Yet, as is clear for Darwin, the decision can be frustrating and has a significant impact on society as a whole if such decisions are correlated.
The decisions of whether to marry or not for most people often depend on other factors, such as economic conditions. Such decisions are often not made by an explicit decision and instead might occur due to circumstances. Nevertheless, such decisions whether made explicitly or implicitly have a large impact on society. Since these decisions are influenced by external factors, as well as by collective changes in attitude such decisions are correlated, which is why they can have a significant impact on others.
Human rights vs. oil
On October 2'nd, 2018, a journalist went to visit his country’s embassy. He went there to obtain documents pertaining to his divorce, so it would be possible for him to marry his fiancé, who was waiting outside. She never saw him again. Indeed, no one saw him leave that embassy. According to reports by journalists and intelligence agencies, this Saudi journalist, Jamal Khashoggi, was murdered as he entered the Saudi embassy in Turkey. After being murdered he was dismembered, and his flesh was put through a meat grinder; in order to be disposed of in small quantities. On November 16, 2018, the CIA concluded that the de facto leader of Saudi Arabia, Mohammed bin Salman (MbS) ordered Khashoggi’s assassination3.
Many people over the world and in the USA considered it a terrible crime (“There will be hell to pay”3). Many called for the USA and other countries to sever their diplomatic relations with Saudi Arabia. However, Donald Trump, the president of the United States at the time of Khashoggi’s murder had doubts about the CIA’s conclusions. He either believed MbS’s claims that he knew nothing about the murder, or more likely did not care.
Saudi Arabia has had a complex relationship with the United States for many years. It has an autocratic Islamic fundamentalist regime, which stands in opposition to the stated values of the USA - a democratic republic, with separation of church and state. In Saudi Arabia there are no guaranteed human rights, and there is no rule of law. People are routinely executed for criticizing the government and can be jailed for many years simply for using social media. Although there currently are sections of the American public who crave such an authoritarian theocracy, this seems to stand in strong contrast to the stated values of the USA.
On the other hand, Saudi Arabia has oil, an awful lot of oil!
Saudi Arabia also buys a lot of arms from the US. Indeed, one of Trumps arguments against sanctioning MbS was that he does not want to endanger 110 billion dollars in arms sales. Although this figure is probably an exaggeration, the fact remains that the USA, or at least some in the USA, have other large financial interests in keeping good relationships with the kingdom.
Oil is still very important for the world’s economy. I live in Houston Texas, and oil is the major source of wealth in Texas. Many people here drive large vehicles and live in large houses, both of which consume large amounts of oil, and their paychecks often depend on the oil business. Saudi Arabia is the world’s largest exporter of oil. While there is a lot of oil in Texas as well, many people from Houston spend time, often years, in the Persian Gulf countries, including Saudi Arabia as part their jobs. Consequently, the USA is an ally of Saudi Arabia, supplying it most of its arms.
Most of the terrorists who boarded the planes that crashed into the World Trade Center and the Pentagon in September 11’th 2001 were from Saudi Arabia, which at the time already raised deep concerns about the close ties between the USA and Saudi Arabia. Moreover, much of the financial support for Islamic fundamentalism and more importantly terrorism came from wealthy people in Saudi Arabia. Yet, this did not cause a significant change in the close relationship between the USA and the Saudi rulers.
The president of the USA at the time was George W. Bush, who’d previously worked in the oil business. His father, a previous US president, also became rich while working in the oil business. Both were close to the Saudi ruling family. They were criticized that their close relationships and business interest with the kingdom affected their decisions. Yet, the relationships between the US and Saudi Arabia did not change significantly after they left office.
In contrast to Trump, Joe Biden, the next president of the USA condemned Khashoggi’s murder. He said: “Jamal Khashoggi and his loved ones deserve accountability. Under a Biden-Harris administration, we will reassess our relationship with the Kingdom, end U.S. support for Saudi Arabia's war in Yemen, and make sure America does not check its values at the door to sell arms or buy oil.” When Biden was elected indeed the relationship between the USA and Saudi Arabia became frosty, it took a long time for the two leaders to meet, and some arm deals were even put on hold.
Then, on July 15, 2022, Biden traveled to Saudi Arabia, met MbS and shook his hand. Why did he do that? Was it simply hypocrisy? This is a possible answer, and one we will consider later. To understand what happened a little historical background is needed. This meeting happened 5 months after Russia invaded Ukraine. This invasion brought the USA in conflict with Putin’s Russia, but it also caused a large spike in oil prices, and a scarcity of natural gas in Europe. Since Saudi Arabia is such a large oil producer, it plays a significant role in the availability and price of oil. High gas and electricity process in turn hurt the world economy, and indirectly the ability to keep a unified front against Russian aggression. Therefore, Saudi Arabia became even more important for the interests of the United States.
To put all of this in the terms used here. Biden when deciding if to meet with MbS, was confronting a frustrating decision. The major frustration here arises from a conflict between values and interests, which sometimes align, but often do not. To be more specific, in this case a conflict between economic interests related to the price and availability of oil, and values such as democratic ideals and human rights. Any decision made in such a case is inherently frustrating, and any decision made has global short-term and long-term implications. If the relationship between the US and Saudi Arabia deteriorated, this could cause an increase in oil prices, possibly hurting the global economy when it was recovering from Covid, among other possible detrimental outcomes. On the other hand, improving these relations without consequences for Khashoggi’s murder will encourage similar acts in the future, both in Saudi Arabia as well as in other allies of the USA.
But in the perfect world
So why can’t everybody just love each other? Or, if we just accept Jesus/Allah/Zeus as our lord and savior all of these problems will be solved. Or, if we just let markets rule there will be no conflicts. Or, if everyone was equal, then we would eliminate all conflicts and frustrations. To summarize, one could claim that frustrations just exist in this imperfect world, and that in a perfect utopia (of ones choosing) such frustrations would be eliminated.
The basic assumption of this work is that such frustrations are inherent. I do not prove this here. However, I believe that there are many structural reasons that in the social and political world conflicts and frustrations are inevitable. First, resources are limited. We might be able to expand resources, over time. However, over a limited span of time and space, resources are inherently limited. This makes competition for such resources natural. Therefore, the interests of different people are likely to be different and this can generate conflict. On top of this people are diverse, they have different ideas of what is good and what is desirable, and these beliefs change over time. This has always been the case. What this diversity of approaches, of values and of opinions, means is that the world that I desire is probably not the one you desire, setting the stage for conflict and for frustrations.
1.2: Notes about The Physics of Frustration
The SodaStream example above is similar to what physicists also call frustration, and in the physics world frustrations are the basic building block of some models of complex systems. Here we will use insights gained from theoretical models called spin glass models1. As is apparent in the name such models are based on a physical property of particles that is called spin. At this point some of you might say, oh spin that’s a physicsy thing, I don’t really understand physics, like E=(MC)2 and that stuff, so maybe I should stop reading here. So please bear with me a little, and I will try to explain this concept in a non-intimidating manner.
Originally, in classical physics, the relevant variable is the angular momentum of rotating objects (Figure 1.2). For example, the earth spins around an axis that goes from the south pole to the north pole. For a rotating object there is a variable called angular momentum. The faster the object rotates the larger this angular momentum. The vector pointing along the axis around which the object is spinning represents the angular momentum, and this can be represented by an arrow along this axis. The faster the object is rotating the longer the arrow. In classical physics, the relevant concept is angular momentum due to actual rotation. For example, in Figure 1 we show this for a rotating sphere such as a planet.
This concept of angular momentum due to objects spinning, is not unique to a rotating planet, any spinning object ha angular momentum, for example a rotating bicycle wheel, or car wheel, or a bullet spinning around its axis when it is shot through a rifle, or a kid on a merry-go-round.
According to electromagnetism, a field of physics, If the rotating sphere has an electric charge, this will create a magnetic field. On the other hand, if charges move in a magnetic field, this will create a force acting on the charges. These observations explain why magnets, or spins might interact. If this is a bit too abstract, you might replace or supplement these concepts with a small home experiment. Pick up two magnets and move them together. You will see that they might attract each other. However, if you flip one of them, then the same magnets will repel each other, and the forces between them might even cause one of them to flip.
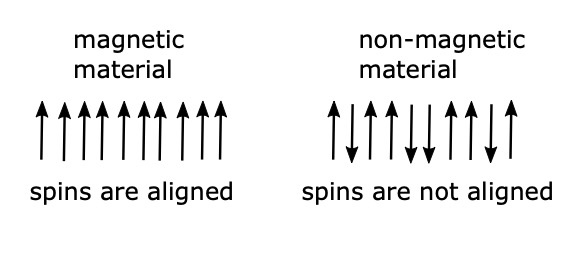
In modern physics though, we talk about ‘spin’ which no longer represents only actual spinning, it becomes an intrinsic property of each particle, it is still related however to magnetization4. In a magnet, or what physicists call a ferromagnet, the spins of the different atoms in the material tend to be aligned, whereas in most other materials they are more or less randomly oriented.
Another difference between spins in classical and modern physics, is that these ‘modern’ spins are no longer continuous variables instead they are discrete. What do I mean by that? An object’s spin around its axis, in 3D space, is represented by an arrow that can point to any direction in and can have any length (Figure 1.2). In contrast the intrinsic spins of particles take on a discrete set of allowed values (they are quantized). In the simplest case, spins can have only two states, denoted here by Up and Down, or represented by the number +1 and -1 respectively. Models using such discreate 2-state spins are called Ising-spin models.
At the microscopic level each of these magnets is composed of a huge number of particles with spins, and when the spins of many of these different particles align (Fig. 1.3), this material becomes a magnet, or what physicists call a ferromagnet. The reason that in some materials spins tend to align depends on the interactions between these spins. Now wait a minute, you might ask, why would spins tend to be aligned? When I spin one bicycle wheel it does not make the other wheel turn around as well? I told you; this physics stuff makes no sense. There are several factors as to why spins might interact, but to start with, think again of the example given above of how two magnets that you hold in your hand interact.
At this point, you might politely ask again - what the fuck! What are these spins, why do they even exist, and why are they discrete? In turn I will politely decline to answer because, hey physics is too complicated (as you knew all along)4, and this is not a physics class. Here, I am just trying to set down some concepts so we can start playing with the metaphor of the world as a frustrated system.
Now some of you might be frustrated because you are incredibly eager to understand how to make the life changing choices of which soda water to buy, and I am talking to you about the earth spinning and about magnets. So, please bear with me for a second, because as we progress, I might be able to convince you that spins would inform us not only about the earth, the universe and everything, but more importantly about choosing soda water.
As briefly stated above, magnets are materials in which spins tend to align, whereas in non-magnetic systems they do not. This is illustrated in Figure 1.3. So, why would spins align in some materials and not in others? It turns out there are forces acting between spins, some of these forces would cause spins to become aligned, in other cases there are forces that could cause them to point in opposite directions. The basis for these forces in physics is complex, but this is not the aim of our game here, because we are not really interested in particles, instead we are interested in soda water. What we care about here is that different types of forces can exist, and the different forces will make spins behave in different ways. Forces that cause spins to become aligned are called ferromagnetic, and those that force them to be in opposite directions are anti-ferromagnetic.
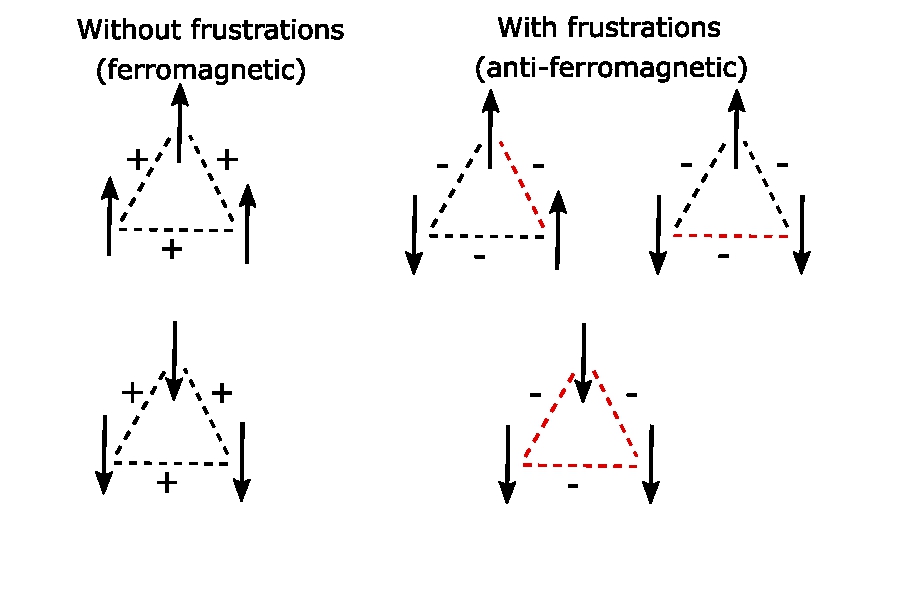
When all bonds are positive (a purely ferromagnetic world) things are relatively simple. There are two equivalent states that the system converges to. In these two states whether all spins point up or all spins point down (Fig. 1.3, left). In both of these cases there are no frustrated bonds because positive sign bonds are not frustrated when both the spins, they connect point in the same direction. These stable states in a physical system are associated with what is called the energy minima of the system (Box 1, Figure 1.5) and the system typically tends to settle in those minima. (Spontaneous symmetry breaking)
On the other hand, consider the case where all bonds are negative as shown in Figure 1.4-right. In this case there is no configuration where all forces (see mathematical inset for a more rigorous definition of force) are aligned with the direction of the spins. Therefore, along some of these connections, the direction of the force would not align with the direction of the spin, such bonds are what physicists call frustrated bonds, and in Figure 1.4 we marked them in red.
Let’s clarify Figure 1.4. The + and – symbols denote the sign of the bond. If it is +, it means that this bond ‘wants’ the two spins it connects to be in the same direction. It does not matter if the direction is ‘UP’ denoted as ↑ or ‘DOWN’ denoted as ↓, as long as they are both the same. If the bond is negative (-), then this bond ‘wants’ both spins to misalign. That is if one is ↑ the other should be ↓. Which spin is ‘UP’ and which is ‘DOWN’ does not matter. If a bond does not get what it ‘wants’ we call it a “frustrated bond”, and paint it in red. Note, that there is a big difference in Figure 1.4, between the two examples in the bottom panels even though in both cases all spins point down. In the example on the left, all bonds are colored in black (not frustrated) and on the right in red (frustrated). The difference is because when all bonds are positive, in the configuration in which all spins point in the same direction (bottom-left) there are no frustrated bonds. In contrast, if all bonds are negative (bottom-right) then when all spins point in the same direction, all bonds are frustrated.
One way to possibly understand this better is to anthropomorphize spins, and the bonds between them. An Ising-spin, as noted can have two states, UP and DOWN. A bond between two spins can be positive or negative. A positive bond wants the spins it connects to be aligned, and then it satisfied, it does not matter it they both point up or both point down. If they point in opposite directions, the positive bond is frustrated. On the other hand, a negative bond is frustrated when both spins point in the same direction. For each spin we can also count how many of the bonds connected to it are frustrated. We can then assign a frustration level to each spin as well. It tuns out, that negative bonds are harder to please.
If the concept of spin still confuses you, think of an example of three kids who can choose to be in either one of two benches in the park. If they all like each other, then we will say the bonds are all positive (ferromagnetic). In this case, all kids will probably choose to be together in one bench, but which bench does not matter. We can label one bench the “UP” bench and the other the “DOWN” bench, to make the analogy more explicit. On the other hand, consider the case where the three kids do not like each other, that is each kid dislikes both other kids. In that case the bonds are all negative (anti-ferromagnetic) and there will be no possible way to make all kids happy. The kid sitting alone at one bench will be happy (though possibly lonely) and the two other kids sitting together will be less happy. Why, because one of their bonds, the bond to the child who is sharing the table with them, will be “frustrated”.
So, what do we learn from this? Well, we reach the deep scientific insight that, well, frustrations suck. You might think though, well we knew that anyway. Bear with me though, because we might be able to get a little more insight when we examine such systems in a little more detail.
Let’s now examine some possible configurations of the 3-spin system (Fig. 1.4, right), when all bonds are negative (-). We see that there are no possible configurations with no frustrated bonds. In the cases where two spins are up and one is down, or when two spins are down and one is up, there is a single frustrated bond (red). In cases where all are UP or all are DOWN, all three bonds are frustrated (Fig. 1.4 bottom, right). From this we learn that there are some conditions that are worse than others (all up or all down), but also that there are multiple conditions that are on average have the same level of frustration (these are also the energy minima of the system). However, even in the cases that are on average equivalent, one spin has no frustrated bonds, while the other two have a single frustrated bond.
Note that this simple 3 spin system is totally ‘egalitarian’, if we can borrow a word not used in physics to describe this system. What do I mean by this? This term here means that all the interacting particles are exactly the same in terms of their bonds, they are all negative and have the same value. Yet, in the final state of the system (minimal energy states) one of the spins has no frustrated bonds, while the other two spins have one frustrated bond. Or to put in more simply, one of the spins will be less frustrated (“happier”) than the other two spins. Which spin ends up ‘happier’ though is completely random, it depends on where we start, and on the random aspects of the process. Though, it is quite likely that if these spins were humans, the happy one would think it’s happier because it is more talented or maybe working harder.
Now let’s look at the behavior of a slightly larger system, which has a mix of positive and negative bonds. We assume here that all spins in this system interact with all other spins with either a positive or a negative sign, chosen randomly. We also assume for the meantime, for simplicity, that the interactions are symmetric, that is spin 1 affects spin 2, is exactly the same way that spin 2 affects spin 1. In physical systems this is typically the case, in the social world not so much. It would be hard to argue for example that my impact on Mark Zuckerberg is the same impact that he has on me. For the time being though, lets stick with this comforting symmetric assumption.
How do we update this system, and what would be the outcomes of such a system? In math box 1, we explain mathematically how such a system is updated. However, we can also explain it intuitively. At each step we choose one spin at random, and we will update the state of that spin. For the updated spin we calculate a property called a field. To calculate this field, we simply first calculate for every other spin the value of its state (either 1 or -1) times the bond strength to the spin we are updating (again either 1 or -1) and then we sum all of these together. If the total sign of the field is positive, we set the value of the chosen spin to UP (+1), and to negative if DOWN (-1). What does this actually do? Each of the other spins tries to force the chosen spin into a specific direction, if the bond is positive it tried to force it to align, and if negative to misalign. The field is the sum of all of these forces, so it can be seen as the net force all other spins direct towards the chosen spin. When we choose the state of the chosen spin, we simply yield to the net force. We keep updating the system by repeatedly and randomly choosing another spin and updating its state. We do this until the state of the system stops changing.
What would then be the outcome of this system? In Figure 1.5 we show such sets of spins, in their initial and final positions. In the frustrated system there are many energy minima, which means that there are many possible spine configurations which are possible in the final state. Another finding would be that despite this update process; there are many frustrated bonds in the final state. We will spend much more time on similar examples in the next chapters, with one difference, the updated variables will no longer be called spins, but children.
1.3 Summary of my claims
I’ve been talking about spins, flipping magnets, and bicycles and mathy things, and by now it’s likely you forgot what this whole thing is about soda water.
Well, hopefully this is more than simply about soda water. In the following chapters I will demonstrate, using a few very simple examples, some general properties of a world that behaves like a frustrated system. I will show that the simple and reasonable assumption that there are conflicts in the world has several general implications:
- Frustrations are inevitable. There is no solution that makes everyone completely happy or un-frustrated; there is no utopia. True, some outcomes can be bad for almost everyone, so there are bad outcomes. However, there is no solution that eliminates all frustrations.
- There are many optimal worlds, but no ideal world. Frustrated systems inherently have many possible outcomes that are equivalent on average. If we search for outcomes that are best on average, there is not one such solution, but very many different solutions with the same average frustration. However, even outcomes that are on average optimal, leave almost everyone with significant frustration.
- Luck has a significant impact on individual levels of frustration. In each outcome, even in each optimal outcome, some people will be less frustrated than others. However, in each one of the equivalent optimal outcomes, the identity of the people who are more frustrated or less frustrated varies. Or in other words, much of what determines how frustrated you are is simply chance, or in other words luck. Note, other factors such as skill are also important, and these have garnered most attention, but luck is also a major factor, and this is inherent to frustrated systems.
- Power differentials make most people very frustrated. Systems in which a small number of the people are much more powerful than most other people will make these privileged people much happier, but they will inevitably increase the average level of frustration.
- Egalitarian systems reduce but do not eliminate frustrations. In egalitarian systems there is less average frustration, but it is not eliminated. There are ways to increase average satisfaction, and these amount to making such systems more egalitarian. In such systems frustrations are not eliminated, they are reduced. However, what this also implies that reducing frustrations of most will inevitably increase the frustrations of some.
1.4 This is not a self-help book, but
This is not a self-help book. There is something pretentious about me giving people advice on how to live their life, when I am not doing such a great job myself. Instead, the aim here is much more modest – to change the world.
I don’t have anything against self-help books if they are indeed honest and effective. Several such books have indeed been helpful to me in the past. Though I claim that this is not a self-help book, there might be a small caveat to this.
When I presented this chapter to a writing group, I was part of, one of the participants, Susan P. said she had struggled with this piece, she wrote: “So why did I struggle? I struggled because of the title and the choice of words. When I first read it, the title did not make sense. Besides, it did not make sense either that the different scenarios were described as “frustrating.” Frustration, as a noun, describes the inner state of the individual “who is upset or annoyed as a result of being unable to change or achieve something.” (Oxford D.). I see frustration as an outcome, even a choice; one's reaction to a challenge.”
I agree with this criticism to a large extent. So why did I use this term? My choice of the word frustration is motivated by its use in physics, more than by its definition in the dictionary. The theory of frustrated systems which arises from physics is the main driving force of this work.
From the disagreement about the meaning of the word frustration I can find one strand of reasoning where this book might serve as a self-help book. I make the claim that in a frustrated system the optimal state, even though one of the best possible on average, is still far from what we want. This is due to inherent conflicts, where a compromise is essential for obtaining optimality. In addition, there are many equivalent alternative states with a similar average outcome. I will demonstrate these statements in the following chapters.
So how does this make this book a self-help book? It is because it might help us accept a reasonable compromise, and it might allow us to see that there are various possible, similarly effective solutions to each problem. These results might allow us to be more flexible and tolerant and indeed make the choice not to be frustrated by such outcomes. Indeed, as Susan implied, it might help us see the inner state of frustration as a choice. If we know we cannot resolve all conflicts, get everything we want, it might be easier to accept the unavoidable conflicts, and maybe be less frustrated about them.
Box 1: Notes about the physics and math of a frustrated system model
Here we outline some of the mathematics used for a simple frustrated system composed of two-state spins. Spin states here are denoted by the variable s. The variable representing the spin of particle i is denoted by s_i. If the spin is in the UP state si=1, if in the DOWN state si=-1. Such binary spins in Physics are called Ising spins. Note that in later chapters this can also denote if a person belongs to one of two classes. In each system the index i runs from 1 to N where N is the number of particles in the system. In statistical mechanics, the branch of physics that deals with such systems, it is often assumed that N is very large, and usually in calculation a limit of N goes to infinity is assumed. This possibly confusing technical detail should not confuse us here, as here no analytical calculations are conducted.
Interactions between spins, or people are captured by the matrix J. In our simple example, Jij denotes the interaction between neurons i and neuron j. In the symmetric case Jij=Jij. The field for each neuron i is captured by the variable . The notation of the form
means a sum over all elements in a list of variables ai
enumerated by the index i.
The decision each spin makes is to be aligned with as many spins that it has a (+1) interaction term with, and to be misaligned with as many that it has a (-1) interaction term with. This means that spin i ‘decides’ to be in the s_i=1 state if h_i>0 and to be in the s_i=-1 state if h_i<0. This decision by the spins defines the dynamics of the system. If each spin is aligned with its field (hi⋅si≥0 for all i) then the system does not change any more or in mathematical terms it reaches a fixed-point.
Another function useful in the analysis of such systems is the so-called Energy function. It is defined as , where the sum is carried out both over the i and j indexes. The decision rule can be proven to always either reduce this energy function or not change it. When the system stops changing it is said to reach a minimum of the energy function. It is hard to depict this energy function as a function of the high-dimensionality space of the variables si where i=1…N. In Figure 1.5B we show schematic 1D projections of such Energy function for different types of systems.
One way to show that the system converges, is by use of the energy function defined above. Such energy functions have minima. In some cases, like in ferromagnets where all interactions are positive (Jij≥0). There are two minima’s where all of the spins are either in the +1 (UP) state or all are in the -1 (DOWN) state. For more complex systems in which the interactions can be both positive and negative, there could be many local minima. By minima we mean that any change of a single spins state will increase the energy. Next, it is easy to show that using the decision process defined above, to flip each spin in the direction of the field, can either reduce or not change the energy function (for the symmetric case where Jij=Jji). I do not show here the detailed mathematical proof, but it can be found in many articles and books including1.
The frustrated model of the magnetic system described here and used extensively in the next chapters is very similar to a model proposed by Sherrington and Kirkpatrick in 1978 (cite). This was a model proposed for disordered magnetic systems called spin-glass. Such models can be simulated on computers, but there are also analytical methods to solve such models. These analytical techniques arise from a field of physics called statistical mechanics. Such solutions do not tell us what each spin is a system does, instead it calculates average statistical properties of such systems. Sherrington and Kirkpatrick used such methods to solve the model they proposed. A comprehensive description of these methods and results for many related models can be found in the book Spin Glass Theory and Beyond1 by Mezard, Parisi and Virasoro, published originally in 1987. Georgio Parisi was awarded the Nobel prize in physics due to his many contributions to the physics of complex systems, including spin-glass theory.
Endnotes - Chapter 1
- The physics and math of spin glass models that are the basis of this book are described in the book: Spin Glass Theory and Beyond by Mezard Parisi and Virasoro (1987). Specifically, the Sherrington-Kirkpatrick (1975) model, included in this book, is closely related to the models in this book. Georgi Parisi Nobel won the Nobel prize in Physics in 2021 for his work on complex systems, including Spin Glass systems. John Hopfield suggested in 1982 that spin glass models could be good models for memory in the Brain. Those models are a little different than the models explored here but share some of their key features. Hopfield won a Nobel prize in Physics for this work in 2024. Some of the newer development in Spin Glass theory are reviewed in the book: Spin Glass Theory and Far Beyond (Charbonneau at al, 2023). This book includes a review of frustrated system models of social and economic systems. Spin Glass models were also used to explain protein folding, by Peter Wolynes and others.
- People’s opinions and actions about SodaStream actually did have an impact. Due to pressure from European customers SodaStream no manufactures in the west bank. As a consequence, many of its employees, both Palestinian and Jewish lost their jobs. On the other hand, is middle east peace any closer?
- The CIA report on the Khashoggi killing determined that the murder was ordered by MbS. The Khashoggi’s murder is described more broadly in the Wikipedia article. and it includes many references. Another interesting article was written soon after the murder by Tom Friedman, who was his friend. The term there will be hell to pay was used by Senator Lindsy Grahm.
- Reference standard QM textbook + popular physics book